For understanding of an object at an advanced evolutionary stage, it is very important to know its metallicity and detailed chemical abundance pattern. Our echelle spectra provide such a possibility due to their large wavelengths coverage.
To study the chemical composition, we have used the
plane-parallel homogeneous models generated by the MARCS program
(Gustafsson et al.1975). It should be noted, however, that
unstable and very extended atmospheres of supergiants probably
require more advanced model atmospheres. Therefore, our results
should be treated as only preliminary ones. For a chemical
composition calculation by the model atmosphere method, one
needs to know the values of the effective temperature (![]() ),
surface gravity (logg) and microturbulent velocity (
),
surface gravity (logg) and microturbulent velocity (![]() ). Determination of
). Determination of ![]() is problematic even for
normal supergiants due to their extended atmospheres and
significant non-LTE effects. In the case of so peculiar a
supergiant as IRAS04296, for which the energy distribution is
strongly distorted by interstellar and circumstellar extinction,
determination of
is problematic even for
normal supergiants due to their extended atmospheres and
significant non-LTE effects. In the case of so peculiar a
supergiant as IRAS04296, for which the energy distribution is
strongly distorted by interstellar and circumstellar extinction,
determination of ![]() is the most difficult problem. We
cannot use for this purpose equivalent widths and profiles of
HI lines (well known criteria of atmospheric conditions for
normal supergiants), since these lines are strongly distorted in
the spectrum of IRAS04296 as seen in Fig.1.
is the most difficult problem. We
cannot use for this purpose equivalent widths and profiles of
HI lines (well known criteria of atmospheric conditions for
normal supergiants), since these lines are strongly distorted in
the spectrum of IRAS04296 as seen in Fig.1.
Therefore, we have applied the spectroscopic method for
temperature determination of IRAS04296, forcing the abundance
derived for each line to be independent on the
lower excitation potential. We have estimated
that ![]() = 6300K with on internal uncertainty
= 6300K with on internal uncertainty
![]()
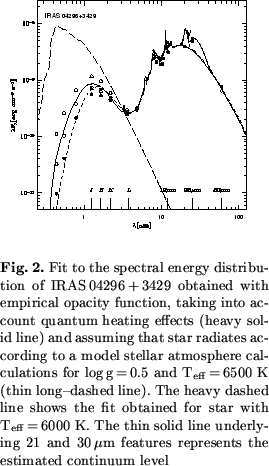 =250K. To check the realiability of our
determination we have modelled the spectral energy distribution
for this source (see Sect.4) and got a very similar
temperature near 6500K. The surface gravity logg=0.0 was
estimated through the ionization balance of the FeI and FeII
abundances. The errors on the parameter logg is determined by forcing a
maximum difference between
=250K. To check the realiability of our
determination we have modelled the spectral energy distribution
for this source (see Sect.4) and got a very similar
temperature near 6500K. The surface gravity logg=0.0 was
estimated through the ionization balance of the FeI and FeII
abundances. The errors on the parameter logg is determined by forcing a
maximum difference between ![]() and
and ![]() to be 0.1dex (where here and hereafter,
to be 0.1dex (where here and hereafter,
![]() ). It should
be noted that the hydrogen abundance
). It should
be noted that the hydrogen abundance ![]() =12.
Such a difference is achieved by varying the logg value
by
=12.
Such a difference is achieved by varying the logg value
by ![]() keeping other parameters
(
keeping other parameters
(![]() and
and ![]() ) constant.
The microturbulent velocity value based on equivalent
widths (W) of FeI and FeII lines is quite high, equal to
7km/s. This value is determined with an uncertainty of
) constant.
The microturbulent velocity value based on equivalent
widths (W) of FeI and FeII lines is quite high, equal to
7km/s. This value is determined with an uncertainty of ![]() , which is typical for F, G-supergiants.
, which is typical for F, G-supergiants.
To illustrate the choice of model parameters for the object IRAS04296 in the Fig.6 are shown the excitation potential - abundance diagram and the equivalent width - abundance diagram for lines of neutral (dots) and ionized (crosses) iron atoms. As follows from this figure, there are not any essential dependences for values considered. The large dispersion is mainly explained by errors of measurement of equivalent widths of weak absorption lines for such a faint object as the IRAS04296 (see, for example, the similar dispersion on the Fig.1 in the paper by Decin et al. (1998) for the brighter object IRAS22223+4327, V=9.7).
We have checked the determination of IRAS04296 model parameters
using weaker FeI and FeII lines and concluded that the
parameters are steady within the erorr box up to
![]() = 100-150mÅ. This can also be seen from Fig.6.
= 100-150mÅ. This can also be seen from Fig.6.
It is well known that the plane-parallel static model atmosphere
method does not give correct abundances for high luminosity
stars (luminosity classes Ia, Ia+). The profiles of the spectral
lines observed are broadened by non-thermal mechanisms whose
influence may be variable at different levels in the atmosphere.
Therefore, to obtain more reliable estimates of chemical element
abundances we use weak lines with ![]() 250mÅ.
The average values of the equivalent widths
250mÅ.
The average values of the equivalent widths ![]() we
used for the abundances calculations are also given in Table1.
Only the BaII abundance was calculated using 3 very strong lines:
we
used for the abundances calculations are also given in Table1.
Only the BaII abundance was calculated using 3 very strong lines:
![]() 5853.67)=464mÅ,
5853.67)=464mÅ,
![]() 6141.71)=679mÅ and
6141.71)=679mÅ and ![]() 6496.90)=738mÅ,
because the weaker lines of this element were not available.
In general, the weak lines formed in deeper atmospheric layers are
more correctly described by the standard static model. The limitation
of equivalent width of lines used to
6496.90)=738mÅ,
because the weaker lines of this element were not available.
In general, the weak lines formed in deeper atmospheric layers are
more correctly described by the standard static model. The limitation
of equivalent width of lines used to ![]() 250mÅ significantly reduces the influence of uncertainty in the choice
of
250mÅ significantly reduces the influence of uncertainty in the choice
of ![]() . Note, however, that the main factor in the abundance
errors for most species remains the uncertainty of the
. Note, however, that the main factor in the abundance
errors for most species remains the uncertainty of the ![]() value.
Therefore, we have checked our estimation of
value.
Therefore, we have checked our estimation of ![]() by modelling of
spectral energy distribution for IRAS04296.
by modelling of
spectral energy distribution for IRAS04296.
Computed abundances of 26 chemical elements are presented in
Table1. In the head of the Table1 parameters of the adopted
model atmosphere are shown. The dependence of chemical
composition determination on uncertanties of the model
atmosphere parameters is discussed in Zacs et al. (1995). In
the second column of Table1 derived abundances are given as
![]() , while in the third column estimated
uncertainties of
, while in the third column estimated
uncertainties of ![]() are shown.
In the next column, the number of spectral lines used for chemical
composition calculation is indicated.
are shown.
In the next column, the number of spectral lines used for chemical
composition calculation is indicated.
| 4c|IRAS04296+3429 | 4c |
|||||||
| 4c| |
4c |
|||||||
| 4c| | 4 | |||||||
| Element | n | n | ||||||
| LiI | 1 | 32 | ||||||
| CI | 8.55 | 0.46 | 21 | 69 | 8.16 | 0.14 | 13 | 47 |
| NI | 7.96 | 0.10 | 4 | 99 | 8.35 | 0.10 | 4 | 127 |
| OI | 8.22 | 0.05 | 3 | 26 | 8.35 | 0.06 | 4 | 23 |
| NaI | 5.91 | 0.24 | 3 | 68 | 6.48 | 0.06 | 4 | 48 |
| MgI | 7.83 | 0.03 | 2 | 56 | ||||
| MgII | 8.08 | 0.03 | 2 | 254 | ||||
| AlI | 6.66 | 0.14 | 3 | 68 | 6.57 | 0.16 | 4 | 32 |
| SiI | 7.29 | 0.20 | 11 | 37 | 7.68 | 0.16 | 16 | 45 |
| SiII | 6.97 | 1 | 22 | 7.81 | 1 | 278 | ||
| SI | 6.80 | 0.21 | 7 | 30 | 7.53 | 0.23 | 2 | 187 |
| CaI | 5.71 | 0.30 | 19 | 98 | 6.41 | 0.22 | 14 | 122 |
| ScII | 2.51 | 0.28 | 10 | 164 | 2.72 | 0.07 | 6 | 119 |
| TiII | 3.91 | 0.33 | 5 | 184 | 4.78 | 0.08 | 4 | 47 |
| VII | 3.26 | 0.28 | 4 | 26 | 3.54 | 0.10 | 4 | 22 |
| CrII | 4.94 | 0.28 | 10 | 108 | 5.54 | 0.12 | 9 | 136 |
| MnI | 5.25 | 0.09 | 3 | 63 | ||||
| FeI | 6.66 | 0.30 | 55 | 75 | 7.48 | 0.21 | 111 | 59 |
| FeII | 6.65 | 0.22 | 19 | 131 | 7.51 | 0.09 | 10 | 154 |
| CuI | 3.61 | 1 | 38 | 4.66 | 1 | 36 | ||
| ZnI | 3.84 | 1 | 9 | |||||
| YII | 2.60 | 0.14 | 2 | 168 | 2.20 | 0.40 | 2 | 32 |
| ZrI | 3.38 | 0.10 | 4 | 6 | ||||
| ZrII | 2.38 | 1 | 165 | |||||
| BaII | 3.78 | 0.47 | 3 | 627 | 2.06 | 1 | 212 | |
| LaII | 1.55 | 0.44 | 6 | 116 | 1.04 | 0.08 | 4 | 20 |
| CeII | 1.53 | 0.16 | 5 | 83 | ||||
| PrII | 0.61 | 1 | 19 | |||||
| NdII | 1.73 | 0.31 | 12 | 102 | 0.84 | 0.08 | 4 | 8 |
| EuII | 0.01 | 0.04 | 2 | 20 | 0.44 | 0.09 | 3 | 20 |
A lot of absorption lines of different elements (CNO-elements, light metals, iron group elements, Ce, Nd, Eu) have been reliably measured in the spectrum of IRAS04296. It is important that we have not found any dependence of the abundances of these species on the equivalent width or on the excitation potential. Therefore the microturbulent velocity does not vary between different chemical elements.
The gf-values for most of the spectral lines used for the abundance calculations were taken from the list used by Luck (1991). The S and CNO-abundances were determined by using the gf-data from Waelkens et al. (1991) and Giridhar et al. (1994). The list of lines with the adopted gf-values, excitation potentials of the lower level and equivalent widths we measured for the object IRAS04296 are available by e-mail ([email protected]).
To verify the method of analysis we observed with the same
spectral device the normal supergiant ![]() Per.
The same procedures for processing and the same list of lines
were used for analysis of the
Per.
The same procedures for processing and the same list of lines
were used for analysis of the ![]() Per spectrum.
This supergiant, whose parameters,
Per spectrum.
This supergiant, whose parameters, ![]() ,
, ![]() ,
, ![]() are very close to
the object studied, is very convenient as a standard for the method
testing because of its membership in the young open cluster
are very close to
the object studied, is very convenient as a standard for the method
testing because of its membership in the young open cluster
![]() which has solar chemical composition
(Klochkova, Panchuk 1985; Boesgaard 1989). Using its membership
of this cluster, we may predict that
which has solar chemical composition
(Klochkova, Panchuk 1985; Boesgaard 1989). Using its membership
of this cluster, we may predict that
![]() also has normal solar chemical composition
(aside from the expected nonsolar CNO triad abundances relative
to iron). As it is shown in Table1
also has normal solar chemical composition
(aside from the expected nonsolar CNO triad abundances relative
to iron). As it is shown in Table1 ![]() has indeed
the abundances of chemical elements close to solar ones, except for
CNO and several elements whose abundances are calculated with a
large uncertainity due to a small number of spectral lines used.
has indeed
the abundances of chemical elements close to solar ones, except for
CNO and several elements whose abundances are calculated with a
large uncertainity due to a small number of spectral lines used.